With our focus on proportional reasoning many educators are discovering that it is everywhere in our math curriculum. Once we become aware of this we know what to look for and listen for so that we can impact students’ fluency and flexibility with numbers.
Recently, I gave the following problem to a Grade 6 class:
How many different rectangles can be made using 36 square tiles each time?
In pairs, students began their investigation. In the past, I have given out squared grid chart paper for students to record on but because we did not have enough of it we did not do that. This turned out to be a good decision for this particular group of students because it pushed them to record dimensions to describe their rectangles rather than spend the time tracing them on the chart paper. From now on I will have some available but I will not make it a requirement.
Once most students had come up with the different rectangles I began the teaching I wanted to do. I asked for the dimensions for each of the rectangles and recorded them so that when we had them all the students could observe some patterns.
Key points brought out through my facilitation of the conversation:
- All of the rectangles had an area of 36 square units.
- A square is a special rectangle.
- Congruent rectangles have similar dimensions e.g., 4×9 and 9×4.
- There is a number relationship between pairs of dimensions (BIG IDEA – Proportional Reasoning)
For example:
half / doubling relationship
2×18 and 4×9 (4 is double 2 and 9 is half 18)
3×12 and 6×6 (3 is half of 6 and 12 is double 6)
third / triple relationship
1×36 and 3×12 (3 is triple 1 and 12 is 1/3 of 36)
This investigation inspired wonderings about what number relationships there would be with rectangles with different areas.
Because I knew the class was working on perimeter as well I asked: If each of these rectangles were gardens which ones would require the least or most amount of fencing to go around? Now we have the opportunity to explore relationships between perimeter and area. Proportional reasoning is everywhere!

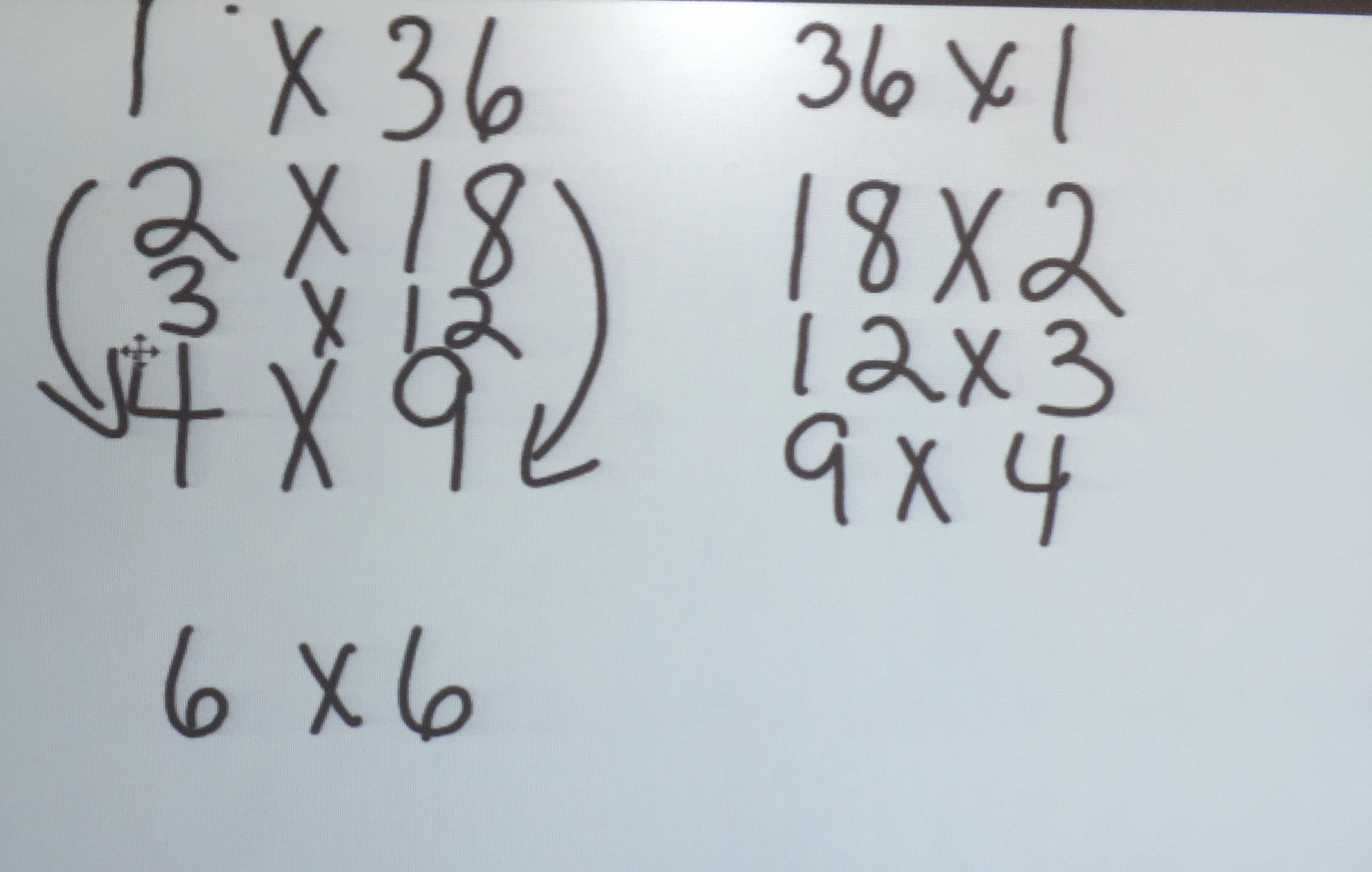
Hello ~ Awesome blog ~ Thank You