Measuring surface area continues to be a challenge for many students in the junior grades. Recently someone was asking me about this, so here are a few thoughts.
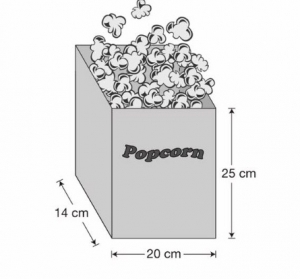
EQAO Problem: The container of popcorn shown is in the shape of a rectangular prism. What is the smallest amount of paper needed to make this container? Show your work.
I chose this problem from a Gr. 6 EQAO Assessment because it is a great example of a question where knowledge, understanding and application of curriculum expectations from Measurement, Geometry and Number Sense are needed to solve it accurately.
One of the biggest challenges for students with this question is understanding exactly what they are measuring. Just as in the early grades where students often confuse area and perimeter, in the upper grades there is often confusion between surface area and volume.
My Thoughts:
I believe the confusion arises because the same dimensions are required for both measurements, but in a different way. When measuring many students often rely on procedures without truly understanding the why behind the appropriate formulas. I also feel that some students in the junior division have challenges with surface area because an understanding of area of a rectangle is not solidified yet.
The words, “What is the smallest amount of paper needed to make this container” indicate that measuring for surface area is required.
This is also a great example of a problem where proportional reasoning can be used to save some steps. For example, if a student decomposes the shape into the five faces, the calculations for the front face can be doubled for the total surface area for the front and back face; the one side doubled to find the total for those two faces. The bottom does not have to be doubled because there is no top. To complete the work, these three measurements need to be added together to find the total surface area of the 3-D shape.
Because the focus of this problem is on surface area and less about whether they can multiply, students who are comfortable using a calculator (and showing their steps) may have less opportunities for error. After all the calculator is only useful if the person using it knows which numbers and symbols to plug in and whether what comes up is reasonable.