Learning about probability provides a great opportunity to revisit fractions and many other important math concepts such as proportional reasoning in a fun way!
Much of this work involves the use of spinners.
Big Ideas
- An experimental probability is based on past events and experiments.
- A theoretical probability is based on an analysis of what could happen.
- In a probability situation, you can never be sure of what will happen next.
- An experimental probability approaches a theoretical probability when enough random samples are used.
How many times should I land on a heart, star or triangle if I spin the spinner 8 times? 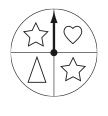
With a task like this you can connect all of the above big ideas e.g., Begin by having students spin the spinner 8 times to find out what happens (experimental probability). If things work out as they should (theoretical probability), then out of 8 spins they will land on stars 4 times and the heart and triangle 2 times each. Of course, in a probability situation we can never be sure what will happen. However, if we use the data from the whole class or have the students do the spinning multiple times (enough random samples), the experimental probability will approach the theoretical probability.
Fractional thinking comes in when students look at the spinner design and notice that there are twice as many stars as triangles and hearts, therefore, half of the total spins should be stars and one-fourth each for the triangle and the heart (8 total spins = 4 spins on the stars, 2 spins on the triangle, and 2 spins on the heart).
Probability is also the perfect opportunity to focus on proportional reasoning. How do the numbers change if the number of spins change from 8 to 16? Sixteen is double 8 so, 4 spins on stars doubles to 8, and 2 each on the triangle and heart, doubles from 2 to 4.
What if we spin 24, 32, or 48 times? Think about the relationships between 8, 16, 24, 32, 48 and use this information to determine the theoretical probability. How might we organize the data on a chart so that we can highlight the number patterns?
In one simple task, we have touched on probability, fractions, division, decomposing numbers, patterning, data management and proportional reasoning.
Wow! Next year wouldn’t it be great to embed probability experiences right from the start of the school year?